线索二叉树
背景: 每次需要知道每个节点的前驱后者后继都需要通过遍历一次二叉树来获得,非常不方便,并且存在很多空的节点,赞成资源浪费;因此线索二叉树应用而生。
一个有 n 个节点的二叉链表,每一个节点有指向左右孩子的两个指针域,总共就是 2n 个指针域。n 个节点的二叉树共同拥有 n-1 条分支线(跟节点没有前驱),存在 2n-(n-1) = n+1 个空指针域。
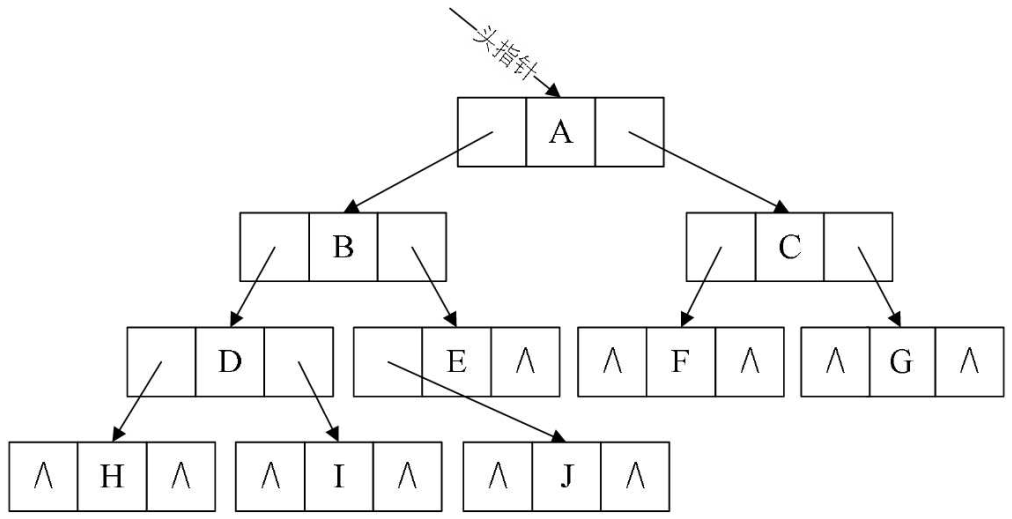
将指向前驱和后继的指针成为线索,加上线索的二叉链表则被叫做线索链表;加上线索的二叉树称为线索二叉树(Threaded Binary Tree)
中序遍历后,将所有的空指针域中的rchild,改为指向它的后继节点。通过指针知道 H 的后继是 D(①),I 的后继是 B (②),J 的后继是 E (③)等等。共有6个空指针域被利用。
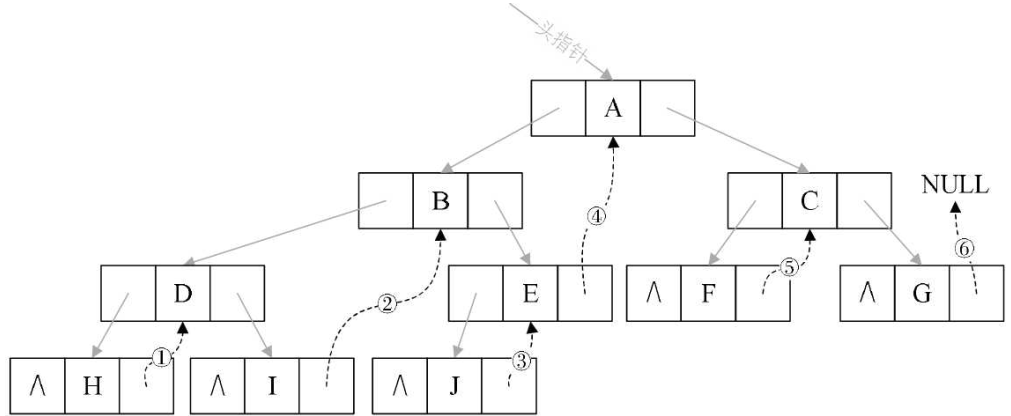
将此棵二叉树的所有空指针域中的lchild,改为指向当前节点的前驱。H 的前驱是NULL(①),I的前驱是D(②),J的前驱是B(③)等等。总共有5个指针域被利用,正好和上面的后继记起来是11个。

线索二叉树,相当于把一颗二叉树变成了一个双向链表,对插入删除节点、查找某个节点都带来了方便。
对二叉树以某种次序遍历使其变为线索二叉树的过程称作为线索化。
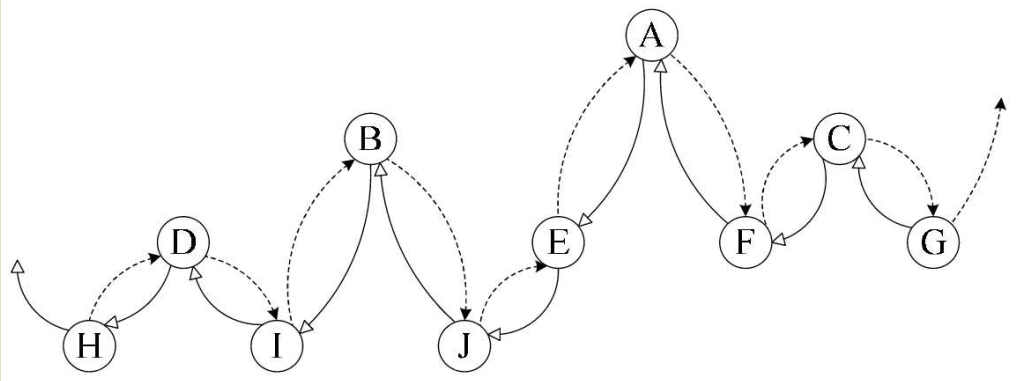
每个节点再增设两个标志域 ltag 和 rtag,ltag 和 rtag只是存放0和1数字的布尔变量,占用空间要小于 lchild 和 rchild 指针域。

- ltag 为0时指向该节点的左孩子,为1时指向该节点的前驱
- rtag 为0时指向该节点的右孩子,为1时指向该节点的后继
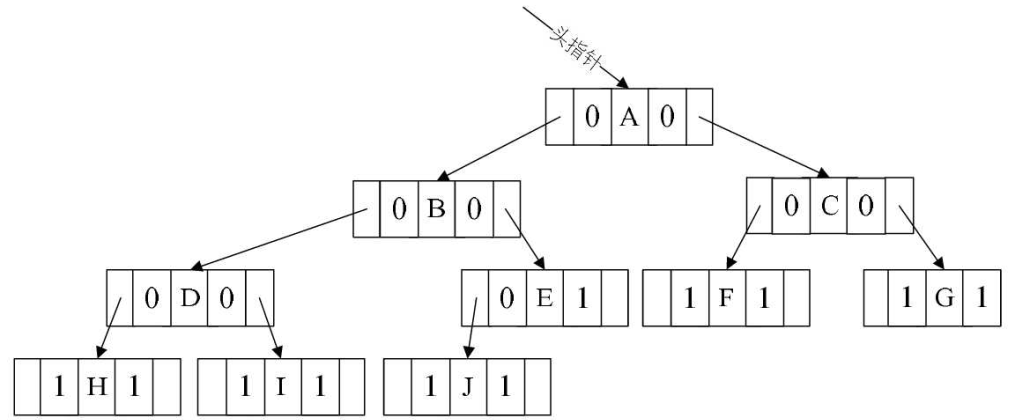
线索二叉树实现
具体代码:
// 节点tag类型,Link表示有子节点,THREAD表示没有字典,其左节点与右节点存储的是线索信息
const pointerTag = {
LINK: Symbol("LINK"),
THREAD: Symbol("THREAD")
};
// 线索二叉树节点信息
class BiTrNode {
constructor(data) {
this.data = data;
// 默认节点类型为Link
this.ltag = pointerTag.LINK;
this.rtag = pointerTag.LINK;
this.lchild = null;
this.rchild = null;
}
/**
* 设置左节点
* @param {Symbol} pointerTag 节点类型
* @param {ThreadTreeNode} lchild 节点信息
*/
setLChild(pointerTag, lchild) {
this.ltag = pointerTag;
this.lchild = lchild;
}
/**
* 设置右节点
* @param {Symbol} pointerTag 节点类型
* @param {ThreadTreeNode} rchild 节点信息
*/
setRChild(pointerTag, rchild) {
this.rchild = pointerTag;
this.rchild = rchild;
}
}
/**
* 线索二叉树数据结构
*/
class BiThrTree {
constructor() {
this.preBiTrTree = null;
// 线索二叉树搜索开始的节点
this.start = null;
// 结束的节点
this.end = null;
}
/**
* 中序遍历二叉树线索化
* @param {BiTrNode} biTrNode 二叉树根节点
*/
inThreading(biTrNode) {
if (biTrNode) {
console.log("当前到达节点" + biTrNode.data);
// 中序遍历左节点
this.inThreading(biTrNode.lchild);
// 如果没有左节点
if (biTrNode.lchild === null) {
console.log(biTrNode.data + " 没有左节点信息");
biTrNode.ltag = pointerTag.THREAD;
biTrNode.lchild = this.preBiTrTree;
// 如果前一个节点为空,则说明此节点是起始点
if (this.preBiTrTree === null) {
this.start = biTrNode;
}
console.log(
biTrNode.data +
" 左节点赋为" +
(this.preBiTrTree == null ? "空指针" : this.preBiTrTree.data)
);
}
// 如果发现前一个节点的左孩子节点为空,则把前一个节点的右孩子节点指向当前节点
if (this.preBiTrTree && this.preBiTrTree.rchild === null) {
console.log(this.preBiTrTree.data + " 没有右节点信息");
this.preBiTrTree.rtag = pointerTag.THREAD;
this.preBiTrTree.rchild = biTrNode;
console.log(
this.preBiTrTree.data +
" 右节点赋为" +
(biTrNode == null ? "空指针" : biTrNode.data)
);
}
this.preBiTrTree = biTrNode;
this.end = biTrNode;
this.inThreading(biTrNode.rchild);
}
}
/**
* 遍历二叉树
* @param {BiTrNode} biTrNode 二叉树根节点
*/
inOrderTraverse(biTrNode) {
this.inThreading(biTrNode);
const T = new BiTrNode(null);
// 设置左节点
T.setLChild(pointerTag.THREAD, this.start);
// 设置右节点
T.setRChild(pointerTag.LINK, this.end);
this.start.lchild = T;
this.end.rchild = T;
let p = T.lchild;
// 如果左节点存在,则一直取左节点的数据
while (p != T) {
while (p.ltag === pointerTag.LINK) {
p = p.lchild;
}
console.log(`${p.data}`);
// 当前如果右边节点存在,且是线索节点,则显示
while (p.rtag === pointerTag.THREAD && p.rchild != T) {
p = p.rchild;
console.log(`${p.data}`);
}
p = p.rchild;
}
}
}
var a = new BiTrNode("a");
var b = new BiTrNode("b");
var c = new BiTrNode("c");
var d = new BiTrNode("d");
var e = new BiTrNode("e");
var f = new BiTrNode("f");
var g = new BiTrNode("g");
var h = new BiTrNode("h");
var i = new BiTrNode("i");
var j = new BiTrNode("j");
a.setLChild(pointerTag.LINK, b);
a.setRChild(pointerTag.LINK, c);
b.setLChild(pointerTag.LINK, d);
b.setRChild(pointerTag.LINK, e);
d.setLChild(pointerTag.LINK, h);
d.setRChild(pointerTag.LINK, i);
e.setLChild(pointerTag.LINK, j);
c.setLChild(pointerTag.LINK, f);
c.setRChild(pointerTag.LINK, g);
const tree = new BiThrTree();
tree.inOrderTraverse(a);
代码分析
-
节点前驱线索化-如果没有左节点,由于其前驱节点已经被访问过,赋值给了 preBiTrTree,所以执行 biTrNode.lchild = this.preBiTrTree
-
节点后继线索化-由于该节点还没访问到,因此需要对它前驱节点 preBiTrTree 的右指针 rchild 做判断,如果 this.preBiTrTree.rchild 等于null,就设置 preBiTrTree.rchild = p,完毕之后节点线索化了
-
this.preBiTrTree = biTrNode;语句的作用是完成前驱和后继的推断后,将当前节点 p 赋值给 pre。以便下一次使用