数据结构-图-章节2

章节2 连通图

图中从一个顶点到另一个顶点，若至少存在一条路径，则称为这两个顶点是想通的。如图1，虽然v1 v3没有直接关联，但从v1到v3存在两条路径，分别是v1-v2-v3和v1-v4-v3，因此v1和v3直接是连通的。

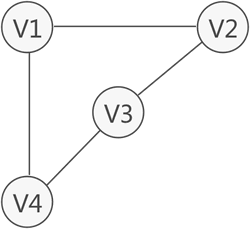图1

无向图中，如果任意两个顶点之间都能够连通，则称此无向图为连通图。例如图2中的无向图就是一个连通图，因此图中的任意两顶点之间都是想通的。

图2

若无向图不是连通图，但是图中的存储的某个子图符合连通图的性质，则称为子图为连通分量。

如图3，虽然3a中的无向图不是连通图，但可以将其分解为3个最大子图如图3b，它们都满足连通图的性质，因此都是连通分量。

图3

需要注意的是，连通分量的提出是以整个无向图不是连通图为前提的，因为如果无向图是连通图，则其无法分解除多个最大连通子图，因此所有的顶点之间都是连通的。

强连通图

有向图中，若任意两个顶点vi和vj，满足从vi到vj以及vj到vi都连通，也就是都含有至少一条通路，则称为强连通图。如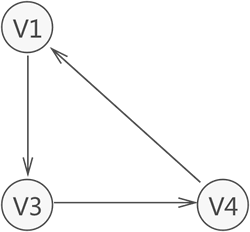图4

图4

与此同时，若有向图本身不是强连通图，但其包含的最大连通子图具有强连通图的性质，则称为子图的强连通分量。

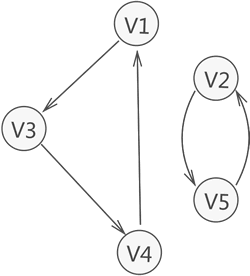图5

总结

可以这样说，连通图是在无向图的基础上对图中的顶点之间的连通做了更高的要求，而强连通图是在有有向图的基础上对图中顶点的连通做了更高的要求。

前端开发 H5 JavaScript 设计模式 browser jQuery 源码分析生活 leetcode Array Stack Queue Linked List 剑指offer Binary Search Tree Binary Tree Breadth-First Search Depth-First Search String Set Binary Search Sliding Window Backtracking Dynamic Programming Two Pointers Union Find Sort Bit Operation Recursion Map Graph Search Hash LinkedList 复盘 QuickSort Trie Design MinHeap Traverse Min Heap Node.js BackEnd SQL MySQL Design Patterns Network 计算机网络 Python SVG