章节4 图的顺序存储结构
使用图结构表示的数据元素之间虽然具有多对多的关系,但是同样可以采用顺序存储,即是采用数组有效存储图。
使用数组表示图时,需要使用两个数组,一个数组存放图中的顶点本身的数据(一维数组),另一个数组存放各顶点之间的关系(二维数组)
不同类型的图,存储的方式略有不同,根据图有无权,可以将图划分为两大类:图和网
图,包括无向图和有向图;网只表示带权的图,包括无向图和有向图。存储方式的不同,指的是:使用二维数组存储图中的顶点之间的关系,如果顶点之间存在边,在相应的位置用1表示,反之用0表示;如果二维数组存储网中的各顶点之间的关系,顶点之间如果有边的存在,在数组的响应位置存储其权值;反之用0表示;
结构代码如下
class Graph {
MAX_VERTEX_NUM = 20; // 顶点的最大个数
VRType = 0; // 表示顶点之间的关系的变量类型
InfoType = ""; // 边的额外信息
VertexType = 0; // 顶点的数据类型
constructor() {
this.vexs = new Array(MAX_VERTEX_NUM); // 顶点数据
this.arcs = []; // 顶点之间的关系
for (let i=0; i<MAX_VERTEX_NUM; i++) {
for (let j=0; j<MAX_VERTEX_NUM; j++) {
this.arcs[i][j] = 0;
}
this.vexnum = 0; // 顶点数目
this.arcnum = 0; // 边的数目
this.kind = ""; // 图的种类
}
}
}
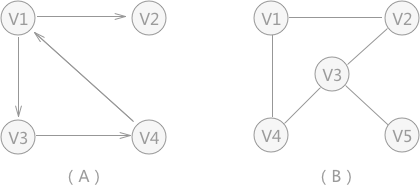
图1 有向图与无向图
例如:图1中无向图,除了存储各顶点本身的数据之外,还需要使用二维数组存储任意两个顶点之间的关系。
由于无向图中没有权值,所以如果两顶点之间有关联,相应位置标为1;反之为0;构建的二维数组如下图所示。

图2 无向图对应的二维数组
在此二维数组中,每一行代表一个顶点,依次从v1到v5,每一列也是如此。比如arcs[0][1] = 1,表示v1和v2之间有边存在;arcs[0][2] = 0,说明v1 和 v3没有边。
对于无向图来说,二维数组构建的二阶矩阵,实际上市对称矩阵,在存储时,就可以采用压缩存储的方式存储下三角或者上三角
通过二阶矩阵,可以直观的判断出各个顶点的度,为该行非0的值的和。例如第一行有两个1,说明v1有两条边。
存储图1中的有向图,对应的二维数组

图3 有向图对应的二维数组arcs
例如:arcs[0][1],证明v1到v2有边的存在。且通过二阶矩阵,可以很轻松得知各顶点入度和出度。即是v1的出度,是该行所有非0值的和为2,v1的入度,是该列所有非0值的和为1。度 = 入度 + 出度 为3
具体代码,js实现如下:
class Graph {
vexnum = 0; // 顶点个数
arcnum = 0; // 边的数量
constructor(vexnum) {
this.vexnum = vexnum;
this.arcs = new Array(vexnum);
for (var i=0; i<vexnum; i++) {
this.arcs[i] = new Array(vexnum);
}
for (let i=0; i<this.vexnum; i++) {
for (let j=0; j<this.vexnum; j++) {
this.arcs[i][j] = {adj: 0, info: null};
}
}
}
printGraph() {
let str = "\n";
for (let i=0; i<this.vexnum; i++) {
for (let j=0; j<this.vexnum; j++) {
str += this.arcs[i][j].adj + " ";
}
str += "\n";
}
return str;
}
}
// 有向图
class CreateDG extends Graph {
isOverBound(v1, v2) {
if (v1 > this.vexnum || v2 > this.vexnum) {
throw new Error("the value is out of bound!");
}
}
// 是否已经存在这样的边
hasEdge(v1, v2) {
return this.arcs[v1][v2].adj === 1;
}
// 添加边
addEdge(v1, v2) {
this.isOverBound(v1, v2);
if (!this.hasEdge(v1, v2)) {
this.arcs[v1][v2].adj = 1;
this.arcnum++;
}
}
}
// 无向图
class CreateDN extends Graph {
isOverBound(v1, v2) {
if (v1 > this.vexnum || v2 > this.vexnum) {
throw new Error("the value is out of bound!");
}
}
// 是否已经存在这样的边
hasEdge(v1, v2) {
return this.arcs[v1][v2].adj === 1;
}
// 添加边
addEdge(v1, v2) {
this.isOverBound(v1, v2);
if (!this.hasEdge(v1, v2)) {
this.arcs[v1][v2].adj = 1;
this.arcs[v2][v1].adj = 1;
this.arcnum++;
}
}
}
// 有向网
class CreateUDG extends Graph {
isOverBound(v1, v2) {
if (v1 > this.vexnum || v2 > this.vexnum) {
throw new Error("the value is out of bound!");
}
}
// 是否已经存在这样的边
hasEdge(v1, v2) {
return this.arcs[v1][v2].adj !== 0;
}
// 添加边
addEdge(v1, v2, w) {
this.isOverBound(v1, v2);
if (!this.hasEdge(v1, v2)) {
this.arcs[v1][v2].adj = w;
this.arcnum++;
}
}
}
// 无向网
class CreateUDN extends Graph {
isOverBound(v1, v2) {
if (v1 > this.vexnum || v2 > this.vexnum) {
throw new Error("the value is out of bound!");
}
}
// 是否已经存在这样的边
hasEdge(v1, v2) {
return this.arcs[v1][v2].adj !== 0;
}
// 添加边
addEdge(v1, v2, w) {
this.isOverBound(v1, v2);
if (!this.hasEdge(v1, v2)) {
this.arcs[v1][v2].adj = w;
this.arcs[v2][v1].adj = w;
this.arcnum++;
}
}
}
// test
var ss = new CreateDG(5);
ss.addEdge(0, 1);
ss.addEdge(2, 1);
ss.addEdge(2, 3);
ss.printGraph();
var ss1 = new CreateDN(5);
ss1.addEdge(0, 1);
ss1.addEdge(2, 1);
ss1.addEdge(2, 3);
ss1.printGraph();
var ss2 = new CreateUDG(5);
ss2.addEdge(0, 1, 1);
ss2.addEdge(2, 1, 2);
ss2.addEdge(2, 3, 3);
ss2.printGraph();
var ss3 = new CreateUDN(5);
ss3.addEdge(0, 1, 1);
ss3.addEdge(2, 1, 2);
ss3.addEdge(2, 3, 3);
ss3.printGraph();
总结:
本章主要介绍了使用数组存储图的方法,在实际操作中使用更多的是链式存储结构,如邻接表、十字链表和邻接多重表