章节 6 深度优先搜索(DFS)和广度优先搜索(BFS)
深度优先搜索
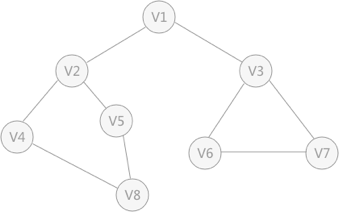
图1 无向图
深度优先搜索的过程类似于树的先序遍历,如图1的过程被分解为: 1 首先任意找到一个未被遍历过顶点,从v1开始,由于v1率先被访问过了,所以需要被标注为已访问。 2 接着遍历v1的邻接点,例如访问v2,并做标志,然后访问v2的邻接点,例如v4,然后v8,然后v5。 3 当v5没有邻接点时,根据之前做的标志显示,所有邻接点都被访问过了。此时,从v5退回到v8,看v8是否有未被访问过的邻接点,如果没有,继续回退到v4,v2,v1。 4 通过查看v1,找到一个未被访问的顶点v3,继续遍历,然后访问v3邻接点v6,然后v7; 5 由于v7没有未被访问的邻接点,所有回退到v6,继续回退至v3,最后到达v1,发现没有未被访问的。 6 最后一步需要判断是否所有顶点都被访问,如果还有没被访问的,以未被访问的顶点为第一个顶点,继续依照上边的方式进行遍历。
根据上边的过程,可以得到遍历次序为: v1-v2-v4-v8-v5-v3-v6-v7
所谓的深度优先搜索,是从图中的一个顶点出发,每次遍历当前访问顶点的邻接点,一直到访问的顶点没有邻接点为止。然后采用回退的方式,查看路上的每一个顶点是否还有其他未被访问的邻接点。访问结束后,判断图中的顶点是否已经全部遍历完成,如果没有,以未访问的顶点为起始点,重复上述过程。
一句话,深度优先搜索是一个不断回溯的过程
js 实现如下:
class AdjacentMatrix {
constructor(vexnum) {
this.vexnum = vexnum;
this.arcs = new Array(vexnum);
for (let i = 0; i < vexnum; i++) {
this.arcs[i] = new Array(vexnum);
}
this.visited = new Array(vexnum).fill(false);
for (let i = 0; i < vexnum; i++) {
for (let j = 0; j < vexnum; j++) {
this.arcs[i][j] = {
adj: 0,
name: "v" + i,
};
}
}
}
isOverBound(v, w) {
if (v >= this.vexnum || w >= this.vexnum) {
throw new Error("vex is over the bound!");
}
}
haveEdge(v, w) {
this.isOverBound(v, w);
return this.arcs[v][w].adj !== 0;
}
addEdge(v, w) {
if (!this.haveEdge(v, w)) {
this.arcs[v][w].adj = 1;
this.arcs[w][v].adj = 1;
}
}
dfs(v, res) {
if (this.visited[v]) {
return;
}
res.push("v" + (v + 1));
this.visited[v] = true;
for (let w = 0; w < this.visited.length; w++) {
if (this.haveEdge(v, w)) {
this.dfs(w, res);
}
}
}
dfsTraverse() {
const res = [];
this.dfs(0, res);
return res.join(" -> ");
}
}
var ss = new AdjacentMatrix(8);
// ss.addEdge(0, 1);
// ss.addEdge(0, 2);
// ss.addEdge(0, 3);
// ss.addEdge(1, 0);
// ss.addEdge(1, 3);
// ss.addEdge(2, 0);
// ss.addEdge(2, 3);
// ss.addEdge(3, 0);
// ss.addEdge(3, 1);
// ss.addEdge(3, 2);
ss.addEdge(0, 1);
ss.addEdge(0, 2);
ss.addEdge(1, 0);
ss.addEdge(1, 3);
ss.addEdge(1, 4);
ss.addEdge(2, 5);
ss.addEdge(2, 6);
ss.addEdge(3, 7);
ss.addEdge(4, 7);
ss.dfsTraverse();
广度优先搜索
广度优先搜索类似于树的层次遍历。从图中的某一顶点触发,遍历每一个顶点时,依次遍历其所有的邻接点,然后再从这些邻接点出发,同样依次访问它们的邻接点。按照此过程,直到图中所有访问过的顶点的邻接点都被访问到。
最后还需要做的操作是查看图中是否还存在未被访问过的顶点,若有,则以该顶点为起始点,重复上述过程遍历即可。
继续拿图1的无向图做例子,假设v1作为起始点,遍历其所有的邻接点v2和v3,以v2为起始点,访问邻接点v4和v5,以v3为起始点,访问邻接点v6和v7,以v4为邻接点访问v8,以v5为起始点,由于v5所有的起始点都已经被访问过,所有直接略过,v6和v7也是如此。 以v1为起始点的遍历过程结束后,判断图中是否还有未被访问的点,由于图1中没有了,所以整个图遍历结束。遍历顶点的顺序为: v1 -> v2 -> v3 -> v4 -> v5 -> v6 -> v7 -> v8
js实现具体如下:
class AdjacentMatrixBFS {
constructor(vexnum) {
this.vexnum = vexnum;
this.arcs = new Array(vexnum);
for (let i = 0; i < vexnum; i++) {
this.arcs[i] = new Array(vexnum);
}
this.visited = new Array(vexnum).fill(false);
for (let i = 0; i < vexnum; i++) {
for (let j = 0; j < vexnum; j++) {
this.arcs[i][j] = {
adj: 0,
name: "v" + i,
};
}
}
}
isOverBound(v, w) {
if (v >= this.vexnum || w >= this.vexnum) {
throw new Error("vex is over the bound!");
}
}
haveEdge(v, w) {
this.isOverBound(v, w);
return this.arcs[v][w].adj !== 0;
}
addEdge(v, w) {
if (!this.haveEdge(v, w)) {
this.arcs[v][w].adj = 1;
this.arcs[w][v].adj = 1;
}
}
bfs(res) {
const queue = [0];
while (queue.length > 0) {
const v = queue.shift();
if (this.visited[v]) continue;
this.visited[v] = true;
res.push("v" + (v + 1));
for (let w = 0; w < this.visited.length; w++) {
if (this.haveEdge(v, w)) {
queue.push(w);
}
}
}
}
bfsTraverse() {
const res = [];
this.bfs(res);
return res.join(" -> ");
}
}
var ss = new AdjacentMatrix(8);
// ss.addEdge(0, 1);
// ss.addEdge(0, 2);
// ss.addEdge(0, 3);
// ss.addEdge(1, 0);
// ss.addEdge(1, 3);
// ss.addEdge(2, 0);
// ss.addEdge(2, 3);
// ss.addEdge(3, 0);
// ss.addEdge(3, 1);
// ss.addEdge(3, 2);
ss.addEdge(0, 1);
ss.addEdge(0, 2);
ss.addEdge(1, 0);
ss.addEdge(1, 3);
ss.addEdge(1, 4);
ss.addEdge(2, 5);
ss.addEdge(2, 6);
ss.addEdge(3, 7);
ss.addEdge(4, 7);
ss.bfsTraverse();
总结:
本章介绍了两种遍历图的方式:深度优先搜索算法和广度优先算法。前者的实现运用的主要是回溯法,类似于树的先序遍历;后者借助队列的先进先出的特点,类似于树的层次遍历。